21. Multiple Integrals in Curvilinear Coordinates

e. Integrating in 3D Curvilinear Coordinates

5. Applications

We previously did Applications of Multiple Integrals in Rectangular Coordinates and we have done Applications of Triple Integrals in Cylindrical Coordinates and Applications of Triple Integrals in Spherical Coordinates. All of those applications can also be done using general 3D curvilinear coordinates.

All the examples on this page of applications of triple integrals in curvilinear coordinates will use the upper half of a torus (donut) where the distance from the center of the hole to the center of the ring is \(4\) and the radius of the ring is \(2\). Find a curvilinear coordinate system for the solid. Then find the ranges of the coordinates to describe the solid and the Jacobian factor.

The plot shows the upper half of a donut.

Slice through the torus vertically at some angle \(\theta\). This gives an \(rz\)-plane which intercets the torus in a circle of radius 2 centered at \((r,z)=(4,0)\). So its equation is \((r-4)^2+z^2=4\) which may be parametrized by: \[ r=4+2\cos\phi \qquad \text{and} \qquad z=2\sin\phi \] If we change the radius of the circle from \(2\) to \(t\) with \(0 \le t \le 2\), we get a smaller circle inside. Putting these together, we get a parametrization of the inside of the original circle as: \[ r=4+t\cos\phi \qquad \text{and} \qquad z=t\sin\phi \]

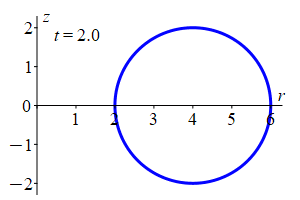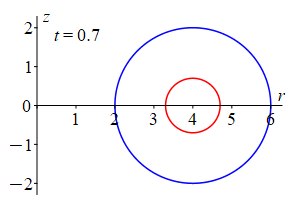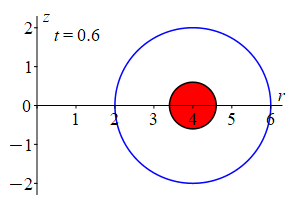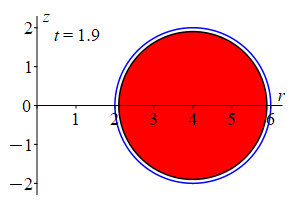
The plot shows a circle of radius 2 in the r z plane for constant theta. The center is at r = 4 and z = 0. In addition there is a circle inside it with radius t which varies between 2 and 0 producing circles which fill the inside of the original circle.

Plugging this into cylindrical coordinates: \[ \vec{R}(r,\theta,z)=\left\langle r\cos\theta,r\sin\theta,z\right\rangle \] we get the toroidal coordinate system: \[ \vec{R}(t,\theta,\phi) =\left\langle (4+t\cos\phi)\cos\theta,(4+t\cos\phi)\sin\theta,t\sin\phi\right\rangle \] The coordinate ranges for the inside of the half-donut are: (Note: \(\phi\) stops at \(\pi\) to give a half circle.) \[ 0 \le t \le 2 \qquad 0 \le \phi \le \pi \qquad 0 \le \theta \le 2\pi \] The coordinate tangent vectors are: \[\begin{aligned} \vec{e}_t&=\dfrac{\partial\vec{R}}{\partial t} =\left\langle \cos\phi\cos\theta,\cos\phi\sin\theta,\sin\phi\right\rangle \\ \vec{e}_\theta&=\dfrac{\partial\vec{R}}{\partial\theta} =\left\langle -(4+t\cos\phi)\sin\theta,(4+t\cos\phi)\cos\theta,0\right\rangle \\ \vec{e}_\phi&=\dfrac{\partial\vec{R}}{\partial\phi} =\left\langle -t\sin\phi\cos\theta,-t\sin\phi\sin\theta,t\cos\phi\right\rangle \end{aligned}\] Then the Jacobian determinant is: (We expand on the second row.) \[\begin{aligned} \dfrac{(x,y,z)}{(t,\phi,\theta)} &=\begin{vmatrix} \cos\phi\cos\theta & \cos\phi\sin\theta & \sin\phi \\ -(4+t\cos\phi)\sin\theta & (4+t\cos\phi)\cos\theta & 0 \\ -t\sin\phi\cos\theta & -t\sin\phi\sin\theta & t\cos\phi \end{vmatrix} \\ &=(4+t\cos\phi)\sin\theta\begin{vmatrix} \cos\phi\sin\theta & \sin\phi \\ -t\sin\phi\sin\theta & t\cos\phi \end{vmatrix} \\ &\quad+(4+t\cos\phi)\cos\theta\begin{vmatrix} \cos\phi\cos\theta & \sin\phi \\ -t\sin\phi\cos\theta & t\cos\phi \end{vmatrix} \\ &=(4+t\cos\phi)\sin\theta\left( t\cos^2\phi\sin\theta+t\sin^2\phi\sin\theta \right) \\ &\quad+(4+t\cos\phi)\cos\theta\left( t\cos^2\phi\cos\theta+t\sin^2\phi\cos\theta \right) \\ &=t(4+t\cos\phi)\sin^2\theta+t(4+t\cos\phi)\cos^2\theta \\ &=t(4+t\cos\phi) \end{aligned}\] And the Jacobian is: \[\begin{aligned} J=t(4+t\cos\phi)=4t+t^2\cos\phi \end{aligned}\] since \(t\) is positive. Finally, the differential of volume is: \[ dV=(4t+t^2\cos\phi)\,dt\,d\phi\,d\theta \]

Volume

Find the volume of the half-donut.

The volume is: \[\begin{aligned} V&=\iint_R 1\,dV =\int_0^{2\pi}\int_0^\pi\int_0^2 (4t+t^2\cos\phi)\,dt\,d\phi\,d\theta \\ &=2\pi\int_0^\pi\left[2t^2+\dfrac{t^3}{3}\cos\phi\right]_0^2\,d\phi =2\pi\int_0^\pi\left(8+\dfrac{8}{3}\cos\phi\right)\,d\phi \\ &=2\pi\left[8\phi+\dfrac{8}{3}\sin\phi\right]_0^\pi =16\pi^2 \end{aligned}\]

Mass

Find the mass of the half-donut if the mass density is \(\delta=z^2\).

Since \(z=t\sin\phi\), the density is: \[ \delta=z^2=t^2\sin^2\phi \] So the mass of the region is given by \[\begin{aligned} M&=\iint\limits_R \delta\,dV =\int_0^{2\pi}\int_0^\pi\int_0^2 t^2\sin^2\phi(4t+t^2\cos\phi)\,dt\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^\pi\int_0^2 (4t^3\sin^2\phi+t^4\sin^2\phi\cos\phi)\,dt\,d\phi\,d\theta \\ &=2\pi\int_0^\pi\left[t^4\sin^2\phi+\dfrac{t^5}{5}\sin^2\phi\cos\phi\right]_0^2\,d\phi \\ &=2\pi\int_0^\pi\left(8(1-\cos2\phi)+\dfrac{32}{5}\sin^2\phi\cos\phi\right)\,d\phi \\ &=2\pi\left[8\left(\phi-\dfrac{\sin2\phi}{3}\right)+\dfrac{32}{5}\dfrac{\sin^3\phi}{3}\right]_0^\pi =16\pi^2 \end{aligned}\]

Center of Mass

Find the center of mass of the half-donut if the mass density is \(\delta=z^2\).

By symmetry, the \(x\) and \(y\) components of the center of mass are \(\bar x=\bar y=0\). So we need to compute the \(z\) component. The \(z\) moment is \[\begin{aligned} M_z&=\iint\limits_R z\,\delta\,J\,du\,dv =\int_0^{2\pi}\int_0^\pi\int_0^2 t^3\sin^3\phi(4t+t^2\cos\phi)\,dt\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^\pi\int_0^2 (4t^4\sin^3\phi+t^5\sin^3\phi\cos\phi)\,dt\,d\phi\,d\theta \\ &=2\pi\int_0^\pi\left[\dfrac{4t^5}{5}\sin^3\phi+\dfrac{t^6}{6}\sin^3\phi\cos\phi\right]_0^2\,d\phi \\ &=2\pi\int_0^\pi\left(\dfrac{128}{5}(1-\cos^2\phi)\sin\phi+\dfrac{32}{3}\sin^3\phi\cos\phi\right)\,d\phi \\ &=2\pi\left[\dfrac{128}{5}\left(-\cos\phi+\dfrac{\cos^3\phi}{3}\right)+\dfrac{32}{3}\dfrac{\sin^4\phi}{4}\right]_0^\pi \\ &=2\pi\left(\dfrac{256}{5}\left(1-\dfrac{1}{3}\right)\right) =\dfrac{1024}{15}\pi \end{aligned}\] So: \[\begin{aligned} \bar z=\dfrac{M_z}{M} =\dfrac{1024\pi}{15}\dfrac{1}{16\pi^2} =\dfrac{64}{15\pi} \end{aligned}\]

Thus the center of mass for this region and given density is \[\begin{aligned} \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{64}{15\pi}\right\rangle \approx\left\langle 0,0,1.36\right\rangle \end{aligned}\] The center of mass is shown as a blue diamond. It is not within the donut (It's in the hole.), but it is within the convex hull.

The plot shows the half donut with a blue diamond in the hole on the z axis.

Centroid

Find the centroid of the half-donut.

Again \(\bar x=\bar y=0\) and we compute \(\bar z\), but this time the density function is \(\delta=1\). The \(z\)-moment of the volume is: \[\begin{aligned} V_z&=\iint\limits_R z\,J\,du\,dv =\int_0^{2\pi}\int_0^\pi\int_0^2 t\sin\phi(4t+t^2\cos\phi)\,dt\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^\pi\int_0^2 (4t^2\sin\phi+t^3\sin\phi\cos\phi)\,dt\,d\phi\,d\theta \\ &=2\pi\int_0^\pi\left[\dfrac{4t^3}{3}\sin\phi+\dfrac{t^4}{4}\sin\phi\cos\phi\right]_0^2\,d\phi \\ &=2\pi\int_0^\pi\left(\dfrac{32}{3}\sin\phi+4\sin\phi\cos\phi\right)\,d\phi \\ &=2\pi\left[-\dfrac{32}{3}\cos\phi+2\sin^2\phi\right]_0^\pi =2\pi\dfrac{64}{3} =\dfrac{128}{3}\pi \end{aligned}\] So: \[\begin{aligned} \bar z=\dfrac{V_z}{V} =\dfrac{128\pi}{3}\dfrac{1}{16\pi^2} =\dfrac{8}{3\pi} \end{aligned}\]

Thus the centroid for this region is: \[\begin{aligned} \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{8}{3\pi}\right\rangle \approx\left\langle 0,0,.849\right\rangle \end{aligned}\] The centroid is shown as a red sphere. It is not within the donut (It's in the hole.), but it is within the convex hull.

The plot shows the half donut with a red sphere in the hole on the z axis.

Since the density \(\delta=z^2\) increases with \(z\) , we expect the center of mass to be above the centroid which it is.

The plot shows the half donut with a blue diamond above a red sphere in the hole on the z axis.

Average Value

Find the average temperature of the half-donut if the temperature is \(T=270-z\).

The average temperature is: \[\begin{aligned} T_\text{ave}&=\dfrac{1}{V}\iiint_R T\,dV =\dfrac{1}{V}\iiint_R 270-z\,dV \\ &=\dfrac{270}{V}\iiint_R 1\,dV-\dfrac{1}{V}\iiint_R z\,dV \end{aligned}\] The first integral is the volume and the second is the \(z\) \(1^\text{st}\) moment of the volume. So: \[ T_\text{ave}=270\dfrac{V}{V}-\dfrac{V_z}{V} =270-\bar z=270-(.849)=269.15 \]

The exercises the rest of this page refer to the upper half of the ellipsoid \(x^2+4y^2+9z^2=36\) discussed on the previous page. We use the same ellipsoidal spherical coordinate system: \[\begin{aligned} x&=6\rho\sin\phi\cos\theta \\ y&=3\rho\sin\phi\sin\theta \\ z&=2\rho\cos\phi \end{aligned}\]

The plot shows the upper half of an ellipsoid which intersects the x axis at plus and minus 6, intersects the y axis at plus and minus 3 and intersects the z axis at plus and minus 2.

For the upper half of the ellipsoid, the bounds are: \[ 0 \le \rho \le 1 \qquad 0 \le \phi \le \dfrac{\pi}{2} \qquad 0 \le \theta \le 2\pi \] (Note: \(\phi\) stops at \(\dfrac{\pi}{2}\) to give the upper half of the ellipsoid.) As discussed on the previous page, the Jacobian is: \[ J=36\rho^2\sin\phi \] which will be derived on the exercise page.

Find the volume of the half ellipsoid.

\(V=24\pi\)

The volume is: \[\begin{aligned} V&=\iiint\limits_R 1\,dV =\iiint\limits_R 36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^{\pi/2}\int_0^1 36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=36\int_0^{2\pi} \,d\theta\int_0^{\pi/2} \sin\phi\,d\phi\int_0^1 \rho^2\,d\rho \\ &=36(2\pi)\left[\rule{0pt}{10pt}-\cos\phi\right]_0^{\pi/2}\left[\dfrac{\rho^3}{3}\right]_0^1 =24\pi \end{aligned}\]

The high school geometry formula for the volume of an ellipsoid is: \[ V=\dfrac{4}{3}\pi \,a\,b\,c =\dfrac{4}{3}\pi \,6\cdot3\cdot2 =48\pi \] Our result is correctly half of this.

Find the mass of the half ellipsoid if the density is \(\delta=z+2\).

\(M=66\pi\)

First, we convert the density function to ellipsoidal spherical coordinates: \[ \delta=z+2=2\rho\cos\phi+2 \] The mass of the ellipsoid is found by integrating the density function over the volume: \[\begin{aligned} M&=\iiint\limits_R \delta\,dV=\iiint\limits_R (2\rho\cos\phi+2)36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=72\int_0^{2\pi}\int_0^{\pi/2}\int_0^1 (\rho^3\sin\phi\cos\phi+\rho^2\sin\phi)\,d\rho\,d\phi\,d\theta \\ &=72\int_0^{2\pi} \,d\theta \left[\int_0^{\pi/2}\sin\phi\cos\phi\,d\phi\int_0^1 \rho^3\,d\rho +\int_0^{\pi/2}\sin\phi\,d\phi\int_0^1 \rho^2\,d\rho\right] \\ &=144\pi \left(\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2}\left[\dfrac{\rho^4}{4}\right]_0^1 +\left[-\cos\phi\dfrac{}{}\right]_0^{\pi/2}\left[\dfrac{\rho^3}{3}\right]_0^1\right) \\ &=144\pi\left[\left(\dfrac{1}{2}\right)\left(\dfrac{1}{4}\right)+(1)\left(\dfrac{1}{3}\right)\right] =144\pi\left(\dfrac{11}{24}\right) =66\pi \end{aligned}\]

Find the center of mass of the half ellipsoid if the density is \(\delta=z+2\).

The center of mass is at:
\(\left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{46}{55}\right\rangle =\langle 0,0,.84\rangle\)

By symmetry \(\bar{x}=\bar{y}=0\). We need to compute \(\bar{z}=\dfrac{M_z}{M}\). We already have the mass of the ellipsoid: \(M=66\pi\). The \(z\)-moment of mass is: \[\begin{aligned} M_z&=\iiint_R z\,\delta\,dV =\iiint_R (2\rho\cos\phi)(2\rho\cos\phi+2)36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=288\pi\int_0^{\pi/2}\int_0^1 (\rho^4\cos^2\phi\sin\phi+\rho^3\cos\phi\sin\phi)\,d\rho\,d\phi \\ &=288\pi\left[\int_0^{\pi/2}\int_0^1 \rho^4\cos^2\phi\sin\phi\,d\rho\,d\phi +\int_0^{\pi/2}\int_0^1 \rho^3\cos\phi\sin\phi\,d\rho\,d\phi\right] \\ &=288\pi\left[\int_0^{\pi/2}\cos^2\phi\sin\phi\,d\phi\int_0^1 \rho^4\,d\rho +\int_0^{\pi/2}\cos\phi\sin\phi\,d\phi\int_0^1 \rho^3\,d\rho\right] \\ &=288\pi\left(\left[\dfrac{-\cos^3\phi}{3}\right]_0^{\pi/2}\left[\dfrac{\rho^5}{5}\right]_0^1 +\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2}\left[\dfrac{\rho^4}{4}\right]_0^1\right) \\ &=288\pi\left[\left(\dfrac{1}{3}\right)\left(\dfrac{1}{5}\right) +\left(\dfrac{1}{2}\right)\left(\dfrac{1}{4}\right)\right] =288\pi\left(\dfrac{23}{120}\right) =\dfrac{276}{5}\pi \end{aligned}\]

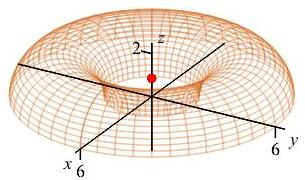
Therefore the \(z\) component of the center of mass is: \[ \bar{z}=\dfrac{M_z}{M} =\dfrac{276\pi}{5}\dfrac{1}{66\pi}=\dfrac{46}{55}=0.84 \] So the center of mass is at: \[\begin{aligned} \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{46}{55}\right\rangle =\langle 0,0,.84\rangle \end{aligned}\] The center of mass is plotted within the half ellipsoid as a blue diamond.

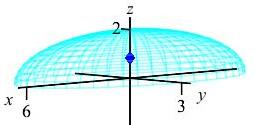
The plot shows the half ellipsoid with a blue diamond on the z axis.

Find the centroid of the half ellipsoid.

The centroid is at:
\(\left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{3}{4}\right\rangle =\langle 0,0,0.75\rangle\)

By symmetry \(\bar{x}=\bar{y}=0\). We need to compute \(\bar{z}=\dfrac{V_z}{V}\). We already have the volume of the half-ellipsoid: \(V=24\pi\). The \(z\)-moment of volume is: \[\begin{aligned} V_z&=\iiint_R z\,dV \\ &=\int_0^{2\pi}\int_0^{\pi/2}\int_0^1 (2\rho\cos\phi)36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=144\pi\int_0^{\pi/2} \cos\phi\sin\phi\,d\phi\int_0^1 \rho^3\,d\rho \\ &=144\pi\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2}\left[\dfrac{\rho^4}{4}\right]_0^1 \\ &=144\pi\left(\dfrac{1}{2}\right)\left(\dfrac{1}{4}\right) =18\pi \end{aligned}\]

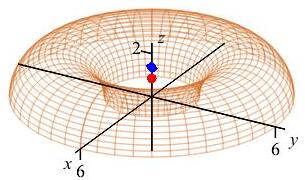
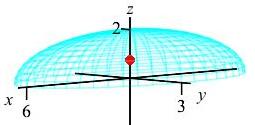
Now we compute \(\bar{z}\) by \[ \bar{z}=\dfrac{V_z}{V} =\dfrac{18\pi}{24\pi}=\dfrac{3}{4}=0.75 \] So the center of mass is at: \[\begin{aligned} \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{3}{4}\right\rangle =\langle 0,0,0.75\rangle \end{aligned}\] The centroid is plotted within the half-ellipsoid as a red sphere.

The plot shows the half ellipsoid with a red sphere on the z axis.

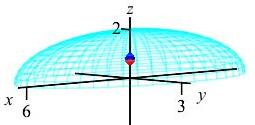
The center of mass is plotted as a blue diamond.
The centroid is plotted as a red sphere.
The center of mass, \(\bar{z}=0.84\), is above the centroid, \(\bar z=.75\), because the density, \(\delta=z+2\), increases with \(z\).

The plot shows the half ellipsoid with a blue diamond above a red sphere, both on the z axis.

Compute the average of the temperature, \(T=270-z^2\), over the ellipsoid.

\(T_\text{ave}=269.2\)

The average temperature is: \[\begin{aligned} T_\text{ave}&=\dfrac{1}{V}\iiint_R T\,dV =\dfrac{1}{V}\iiint_R 270-z^2\,dV \\ &=\dfrac{270}{V}\iiint_R 1\,dV-\dfrac{1}{V}\iiint_R z^2\,dV \end{aligned}\] The first integral is the volume and the second is: \[\begin{aligned} \iiint_R z^2\,dV &=\int_0^{2\pi}\int_0^{\pi/2}\int_0^1 (2\rho\cos\phi)^2 36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=288\pi\int_0^\pi \cos^2\phi\sin\phi\,d\phi\int_0^1 \rho^4\,d\rho \\ &=288\pi\left[\dfrac{-\cos^3\phi}{3}\right]_0^{\pi/2}\left[\dfrac{\rho^5}{5}\right]_0^1 \\ &=288\pi\left(\dfrac{1}{3}\right)\left(\dfrac{1}{5}\right) =\dfrac{96}{5}\pi \end{aligned}\] Since \(V=24\pi\), we have: \[\begin{aligned} T_\text{ave}&=270\dfrac{V}{V}-\dfrac{1}{V}\iiint_R z^2\,dV \\ &=270-\dfrac{1}{24\pi}\dfrac{96\pi}{5} =270-\dfrac{4}{5} =269.2 \end{aligned}\]

© MYMathApps

Supported in part by NSF Grant #1123255