21. Multiple Integrals in Curvilinear Coordinates

c. Integrating in Spherical Coordinates

2. Integral over a Spherical Region

We now explore integration in spherical coordinates with constant and non-constant limits.

Integral over a Spherical Box

We now want to integrate over the spherical box: \[ \rho_1 \le \rho \le \rho_2 \qquad \phi_1 \le \phi \le \phi_2 \qquad \theta_1 \le \theta \le \theta_2 \] Using the Riemann Sum definition with \(\Delta V_{ijk}={\rho_i^*}^2\sin\phi_j^*\,\Delta\rho_i\,\Delta\phi_j\,\Delta\theta_k\), the integral is: \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\lim_{p\rightarrow\infty} \lim_{q\rightarrow\infty} \lim_{r\rightarrow\infty} \sum_{i=1}^p\sum_{j=1}^q\sum_{k=1}^s f(\rho_i^*,\phi_j^*,\theta_k^*) {\rho_i^*}^2\sin\phi_j^*\,\Delta\rho_i\,\Delta\phi_j\,\Delta\theta_k \] We recognize this as the triple iterated integral: \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\theta_1}^{\theta_2}\int_{\phi_1}^{\phi_2}\int_{\rho_1}^{\rho_2} f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \] By Fubini's Theorem, there are five other orders of integrations obtained by reordering the differentials and the corresponding limits.

Other Integrals in Spherical Coordinates

In addition to integrating over spherical boxes, spherical coordinates can be used to integrate over other types of regions with appropriate definitions of the regions. The resulting integrals have the forms:

Type \(\rho\theta\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\rho_1}^{\rho_2}\int_{g(\rho)}^{h(\rho)}\int_{p(\rho,\theta)}^{q(\rho,\theta)} f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\phi\,d\theta\,d\rho \] Type \(\theta\rho\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\theta_1}^{\theta_2}\int_{g(\theta)}^{h(\theta)} \int_{p(\rho,\theta)}^{q(\rho,\theta)} f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\phi\,d\rho\,d\theta \] Type \(\rho\phi\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\rho_1}^{\rho_2}\int_{g(\rho)}^{h(\rho)}\int_{p(\rho,\phi)}^{q(\rho,\phi)} f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\theta\,d\phi\,d\rho \] Type \(\phi\rho\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\phi_1}^{\phi_2}\int_{g(\phi)}^{h(\phi)} \int_{p(\rho,\phi)}^{q(\rho,\phi)} f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\theta\,d\rho\,d\phi \] Type \(\theta\phi\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\theta_1}^{\theta_2}\int_{g(\theta)}^{h(\theta) }\int_{p(\theta,\phi)}^{q(\theta,\phi) }f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \] Type \(\phi\theta\): \[ \iiint\limits_R f(\rho,\phi,\theta)\,dV =\int_{\phi_1}^{\phi_2}\int_{g(\phi)}^{h(\phi)} \int_{p(\theta,\phi)}^{q(\theta,\phi) }f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\theta\,d\phi \]

Notice that each integral can have limits which depend only on the variables outside that integral.

Find the volume of the orange wedge given in spherical coordinates by \(0 \le \rho \le 5\), \(0 \le \theta \le \dfrac{\pi}{6}\), and \(0 \le \phi \le \pi\).

This is how the wedge looks:

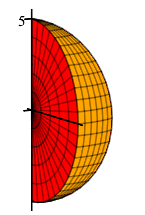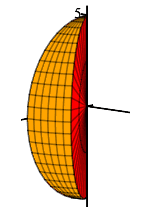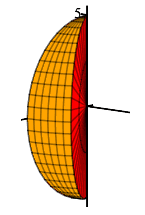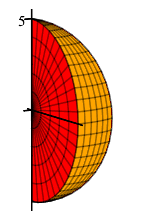
This is a straightforward application of integration in spherical coordinates. Our integral with limits is as follows: \[\begin{aligned} V&=\int_0^{\pi/6}\int_0^\pi\int_0^5 \rho^2\sin\phi\,d\rho\,d\phi\,d\theta =\int_0^{\pi/6}\int_0^\pi \left[\dfrac{\rho^3}{3}\right]_{\rho=0}^5\sin\phi\,d\phi\,d\theta \\ &=\dfrac{125}{3}\int_0^{\pi/6}\int_0^\pi \sin\phi\,d\phi\,d\theta =\dfrac{125}{3}\int_0^{\pi/6}\int_0^\pi \sin\phi\,d\phi\,d\theta \\ &=\dfrac{125}{3}\int_0^{\pi/6} \left[-\cos\phi\right]_{\phi=0}^\pi\,d\theta =\dfrac{125}{3}(2)\int_0^{\pi/6} \,d\theta \\ &=\dfrac{250}{3}\cdot\dfrac{\pi}{6} =\dfrac{125}{9}\pi \end{aligned}\]

We should have known this answer. Since \(\dfrac{\pi}{6}\) is \(\dfrac{1}{12}\) of a full circle \(2\pi\), the wedge is \(\dfrac{1}{12}\) of a sphere and its volume is \(\dfrac{1}{12}\) of the volume of a sphere of radius \(5\): \(V= \dfrac{1}{12}\dfrac{4}{3}\pi(5)^3=\dfrac{125}{9}\pi\). However, it is useful to write down the triple integral for the volume so we can use it to find the integrals for average value, centroid, mass, and center of mass.