22. Parametric Surfaces and Surface Integrals

b. Tangent and Normal Vectors

1. Coordinate Curves

For a 2D curvilinear coordinate system \(\vec R(u,v)\), the coordinate curves (the \(u\)-curves and \(v\)-curves) are obtained by holding one coordinates fixed while the other coordinate changes. \(u\) changes on a \(u\)-curve. \(v\) changes on a \(v\)-curve.

In the figure the blue curves are the \(u\)-curves and the red curves are the \(v\)-curves.

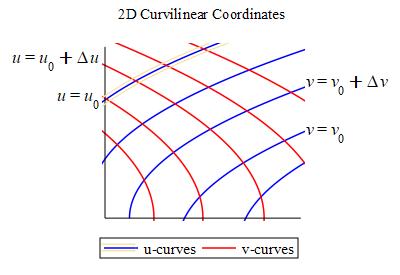
The plot shows two sets of intersecting curves called the general curvilinear coordinate system. The first set are decreasing and bending down, two of which are labeled u = u sub 0 and u = u sub 0 + Delta u. The second set are increasing and bending down, two of which are labeled v = v sub 0 and v = v sub 0 + Delta v. They form the outline of a curved rectangle.

For a parametric surface, \(\vec R(u,v)\), the coordinate curves (the \(u\)-curves and \(v\)-curves) are obtained by holding one coordinate fixed while the other coordinate changes. \(u\) changes on a \(u\)-curve. \(v\) changes on a \(v\)-curve.
The \(u\)-curve with \(v=v_0\) and parameter \(u\) is: \[ \vec R(u,v_0)=\left\langle x(u,v_0),y(u,v_0),z(u,v_0)\right\rangle \] The \(v\)-curve with \(u=u_0\) and parameter \(v\) is: \[ \vec R(u_0,v)=\left\langle x(u_0,v),y(u_0,v),z(u_0,v)\right\rangle \]

Parametric Surface
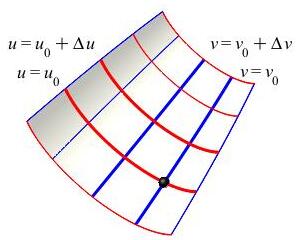
The plot shows a curved surface with 5 blue lines crossed by 5 red lines. 2 of the blue lines are darker and labeled v = v sub 0 and v = v sub 0 plus Delta v. 2 of the red lines are darker and labeled u = u sub 0 and u = u sub 0 plus Delta u.

In the figure the blue curves are the \(u\)-curves and the red curves are the \(v\)-curves.

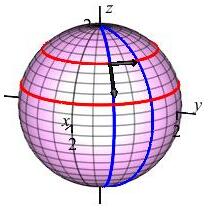
Identify the coordinate curves for the sphere of radius \(\rho=2\), parametrized by \[ \vec R(\phi,\theta) =\left\langle 2\sin\phi\cos\theta,2\sin\phi\sin\theta,2\cos\phi\right\rangle \]

A \(\phi\)-curve is a line of longitude (in blue) increasing from the North pole to the South pole with a constant value of \(\theta\). A \(\theta\)-curve is a line of latitude (in red) increasing from West to East with a constant value of \(\phi\).

The plot shows a sphere with two blue lines from the North pole to the South pole and an arrow pointing South. It also shows two red lines making horizontal circles on the sphere and an arrow pointing East.

Identify the coordinate curves for the paraboloid \(z=\dfrac{x^2+y^2}{5}\) parametrized by \(\vec R(r,\theta) =\left\langle r\cos\theta,r\sin\theta,\dfrac{r^2}{5}\right\rangle\).

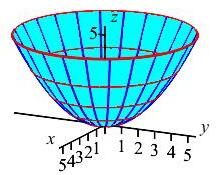
The plot shows a bowl shape whose top edge is a horizontal circle.

The \(r\)-curves are the parabolas (in blue).
The \(\theta\)-curves are the circles (in red).

An \(r\)-curve is a parabola (in blue) starting at the vertex of the paraboloid and increasing up a side with a constant value of \(\theta\). A \(\theta\)-curve is a circle (in red) increasing counterclockwise around the paraboloid with a constant value of \(r\).

Notice the boundary curves affect the choice of parametrization, but they do not affect the coordinate curves.

© MYMathApps

Supported in part by NSF Grant #1123255