7. Trigonometric Substitutions

Homework

Evaluate each integral. Be sure to check your answer by differentiating, unless it is a definite integral.

1. \(\displaystyle \int \dfrac{\sqrt{1-x^2}}{x^2}\,dx \)

2. \(\displaystyle \int\dfrac{x^2}{\left(1+x^2\right)^{3/2}}\,dx\)
   NOTE: There's massive algebra to check your antiderivative!

3. \(\displaystyle \int \dfrac{1}{x^2\sqrt{x^2-1}}\,dx \)

4. \(\displaystyle \int_{\sqrt{2}}^2 \dfrac{x}{1-x^2}\,dx \)  You must use a trig substitution. Check with an ordinary substitution.

5. \( \displaystyle \int_{1/2}^{\sqrt{2}/2} \dfrac{x}{x^2-1}\,dx \)  You must use a trig substitution. Check with an ordinary substitution.

6. >

   \( \displaystyle \int \dfrac{\sqrt{9x^2-16}}{x}\,dx \)

7. \(\displaystyle \int \dfrac{x^2}{(4-25x^2)^{3/2}}\,dx\)

8. \(\displaystyle \int \dfrac{4}{(4+9x^2)^{3/2}}\,dx\)

9. \(\displaystyle \int \dfrac{dx}{\sqrt{x^2+6x+5}}\)

10. Use a hyperbolic trig substitution to compute \(\displaystyle \int \dfrac{x^2}{\sqrt{1+x^2}}\,dx\) (Honors Only)

11. Find the average value of the function \(f(x)=\sqrt{4-x^2}\) on the interval \([-1,1]\).

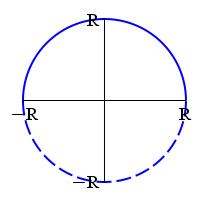
12. Prove the area of a circle of radius \(R\) is \(A=\pi R^2\) by computing the integral \(\displaystyle \int_{-R}^{R} \sqrt{R^2-x^2}\,dx\).